Campo magnético producido por un solenoide

Calculamos el campo producido por un solenoide en un punto P situado en el eje del solenoide:

• Sumando el campo producido por las N espiras en un punto de su eje común.
• Aplicando la ley de Ampère, a un solenoide muy largo comparado con el radio de sus espiras

Campo producido por un solenoide en un punto de su eje

Vamos a calcular el campo producido por el solenoide en un punto P situado en el eje del solenoide sumando el campo producido por las N espiras.

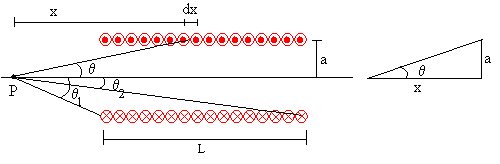
En la figura, tenemos un corte longitudinal de un solenoide de longitud L, formado por N espiras iguales de radio a.

En la página titulada, campo magnético producido por una espira, obtuvimos la expresión del campo magnético producido por una espira de radio a en un punto P de su eje distante x.

B=μ0ia22(a2+x2−−−−−−√)3${\displaystyle B=\frac{{\mu }_{0}i{a}^2}{2{\left(\sqrt{a^2+x^2}\right)}^3}}$

Todas las espiras del solenoide producen en P un campo que tiene la misma dirección y sentido, pero distinto módulo, dependiendo de su distancia x al punto P.

El número de espiras que hay en el intervalo comprendido entre x y x+dx es dn=N·dx/L

Estas espiras producen en P un campo que es el producto del campo producido por una espira por el número dn de espiras

dB=μ0ia22(a2+x2−−−−−−√)3NLdx${\displaystyle dB=\frac{{\mu }_{0}i{a}^2}{2{\left(\sqrt{a^2+x^2}\right)}^3}\frac{N}{L}dx}$

Para integrar, tenemos que hacer el cambio de variablea=x·tanθ y teniendo en cuenta que, 1+tan²θ =1/cos²θ, simplificamos la integral

B=μ0iN2L∫θ1θ2−sinθ⋅dθ=μ0iN2L(cosθ2−cosθ1)${\displaystyle B=\frac{{\mu }_{0}iN}{2L}{\displaystyle \underset{{\theta }_1}{\overset{{\theta }_2}{\int }}-\sin \theta ·d\theta }=\frac{{\mu }_{0}iN}{2L}\left(\cos {\theta }_2-\cos {\theta }_1\right)}$

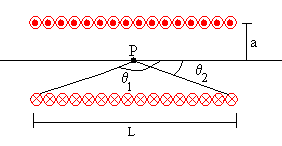
Si el solenoide es muy largo comparado con su radio a y si el punto P está situado en el centro, tendremos que θ1→π y θ2→0${\theta }_1\to \pi \text{y}{\theta }_2\to 0$. El campo B vale entonces

B=μ0iNL${\displaystyle B=\frac{{\mu }_{0}iN}{L}}$

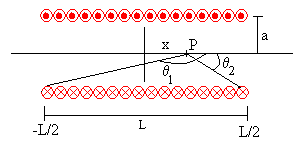
Representamos ahora, el campo B en unidades del campo en el centro del solenoide, en función de la posición x del punto P, situando el origen de coordenadas en el centro del solenoide, tal como se muestra en la figura, más abajo.

BB0=12(cosθ2−cosθ1) cosθ2=L/2−x(L/2−x)2+a2√  cosθ1=−L/2−x(−L/2−x)2+a2√

Mas info: /solenoide/solenoide.html